Contando sujetos y analizando los resultados (II)
Decíamos en el anterior número que en los próximos capítulos íbamos a tratar de obtener información a partir de datos obtenidos por conteos. Habitualmente, en nuestra práctica diaria obtenemos muchos procedentes de contajes (por ejemplo, individuos):
■ El porcentaje de mortalidad de una granja, contando
los cerdos muertos.
■ El porcentaje de abortos, contando el número
de cerdas que abortan.
■ Y así, en un sinfín de variables.
Lo que hacemos es obtener datos de variables explicativas y los comparamos, bien con unos valores estándar o bien con unos valores esperados.
Veamos la lógica del análisis de unos datos procedentes de conteos.
LA TEORÍA DEL ANÁLISIS DE LOS CONTEOS
Imaginemos los siguientes datos, tan simples como que en un corral tenemos 47 lechones provenientes de 4 cerdas y tenemos 29 machos y 18 hembras. Esta distribución de sexos, ¿es diferente para decir que no provienen de una población donde la proporción de hembras y machos es la misma?Vamos a verlo.
En una población donde la proporción de hembras y machos fuese del 50 %, en este ejemplo tendríamos 23 o 24 lechones de cada sexo. A efectos matemáticos diríamos que son 23,5. Con un simple test de Chi-cuadrado podemos contestar a la pregunta anterior.
Recordemos que nuestro estadístico Chi-cuadrado se calcula con la fórmula:
El valor de la distribución Chi-cuadrado con un grado de libertad es 3,841. Este valor se puede hallar en las tablas de distribución de Chi-cuadrado o bien en Excel mediante la fórmula =PRUEBA.CHI.INV(0,05;1). Como nuestro valor es menor podemos concluir que a pesar de todo, no podemos rechazar la hipótesis de que la distribución de sexos es 50:50.
OTRA FORMA DE SABER SI ACEPTAR O RECHAZAR
Si abrimos un archivo Excel y escribimos =DISTR.CHI(2,5745;1), el resultado es la probabilidad de la distribución Chi-cuadrado, que en nuestro caso es igual a 0,1086, es decir, p = 0,1086. Como siempre manejamos un error correspondiente a p=0,05.Este resultado nos dice (de nuevo) que debemos aceptar la hipótesis nula, que en nuestro caso es que la distribución de sexos era 50:50.
Ahora con R
¿Cómo lo haríamos con R? Abrimos R y en la consola principal, antes de ir a RCommander, escribimos:

y obtendremos:
que como podéis apreciar es lo mismo que hemos hecho en Excel.
GRÁFICOS
 Vamos a verlo en un gráfico. La figura 1 es la representación de la función Chi-cuadrado para un grado de libertad. En el eje X (horizontal) vemos los valores que va tomando el valor de
Vamos a verlo en un gráfico. La figura 1 es la representación de la función Chi-cuadrado para un grado de libertad. En el eje X (horizontal) vemos los valores que va tomando el valor de
Chi-cuadrado para las diferentes densidades de la función. El histograma y una línea verde representan precisamente la distribución de Chi-cuadrado. La línea roja marca el valor a partir del cual (a la derecha) si nuestro valor Chi-cuadrado (en este caso 2.5475) hubiera estado más allá, hubiera sido significativo (esa región es el 5 % del área bajo la curva). Como nuestro valor está situado en la línea negra (izquierda de la línea roja), está en la zona 95 %, por lo que no tenemos motivos para rechazar la hipótesis nula. Este gráfico está construido con el siguiente conjunto de instrucciones:
TEST BINOMIAL EN R
Como en este ejemplo la variable sólo puede tomar dos valores (macho o hembra), también hubiéramos podido analizar estos datos mediante un test binomial. Si escribimos de nuevo en la consola:
■ El porcentaje de mortalidad de una granja, contando
los cerdos muertos.
■ El porcentaje de abortos, contando el número
de cerdas que abortan.
■ Y así, en un sinfín de variables.
Lo que hacemos es obtener datos de variables explicativas y los comparamos, bien con unos valores estándar o bien con unos valores esperados.
Veamos la lógica del análisis de unos datos procedentes de conteos.
LA TEORÍA DEL ANÁLISIS DE LOS CONTEOS
Imaginemos los siguientes datos, tan simples como que en un corral tenemos 47 lechones provenientes de 4 cerdas y tenemos 29 machos y 18 hembras. Esta distribución de sexos, ¿es diferente para decir que no provienen de una población donde la proporción de hembras y machos es la misma?Vamos a verlo.
En una población donde la proporción de hembras y machos fuese del 50 %, en este ejemplo tendríamos 23 o 24 lechones de cada sexo. A efectos matemáticos diríamos que son 23,5. Con un simple test de Chi-cuadrado podemos contestar a la pregunta anterior.
Recordemos que nuestro estadístico Chi-cuadrado se calcula con la fórmula:
y si aplicamos nuestros valores:
El valor de la distribución Chi-cuadrado con un grado de libertad es 3,841. Este valor se puede hallar en las tablas de distribución de Chi-cuadrado o bien en Excel mediante la fórmula =PRUEBA.CHI.INV(0,05;1). Como nuestro valor es menor podemos concluir que a pesar de todo, no podemos rechazar la hipótesis de que la distribución de sexos es 50:50.
OTRA FORMA DE SABER SI ACEPTAR O RECHAZAR
Si abrimos un archivo Excel y escribimos =DISTR.CHI(2,5745;1), el resultado es la probabilidad de la distribución Chi-cuadrado, que en nuestro caso es igual a 0,1086, es decir, p = 0,1086. Como siempre manejamos un error correspondiente a p=0,05.Este resultado nos dice (de nuevo) que debemos aceptar la hipótesis nula, que en nuestro caso es que la distribución de sexos era 50:50.
Ahora con R
¿Cómo lo haríamos con R? Abrimos R y en la consola principal, antes de ir a RCommander, escribimos:

y obtendremos:
que como podéis apreciar es lo mismo que hemos hecho en Excel.
GRÁFICOS
 Vamos a verlo en un gráfico. La figura 1 es la representación de la función Chi-cuadrado para un grado de libertad. En el eje X (horizontal) vemos los valores que va tomando el valor de
Vamos a verlo en un gráfico. La figura 1 es la representación de la función Chi-cuadrado para un grado de libertad. En el eje X (horizontal) vemos los valores que va tomando el valor deChi-cuadrado para las diferentes densidades de la función. El histograma y una línea verde representan precisamente la distribución de Chi-cuadrado. La línea roja marca el valor a partir del cual (a la derecha) si nuestro valor Chi-cuadrado (en este caso 2.5475) hubiera estado más allá, hubiera sido significativo (esa región es el 5 % del área bajo la curva). Como nuestro valor está situado en la línea negra (izquierda de la línea roja), está en la zona 95 %, por lo que no tenemos motivos para rechazar la hipótesis nula. Este gráfico está construido con el siguiente conjunto de instrucciones:
TEST BINOMIAL EN R
Como en este ejemplo la variable sólo puede tomar dos valores (macho o hembra), también hubiéramos podido analizar estos datos mediante un test binomial. Si escribimos de nuevo en la consola:
donde nos informa de que nuestra proporción de
machos y hembras 0,50 (o 50 %) está dentro del intervalo de confianza [0,46-0,75], con un valor de p ligeramente superior (0,1439) en esta aproximación. Tenemos que tener en cuenta que si la proporción esperada no es 50:50 es necesario incluir el parámetro en la orden: por ejemplo, “binom.test(observado, p=0.25)”.
machos y hembras 0,50 (o 50 %) está dentro del intervalo de confianza [0,46-0,75], con un valor de p ligeramente superior (0,1439) en esta aproximación. Tenemos que tener en cuenta que si la proporción esperada no es 50:50 es necesario incluir el parámetro en la orden: por ejemplo, “binom.test(observado, p=0.25)”.
CHI-CUADRADO PARA LA BONDAD DE AJUSTE
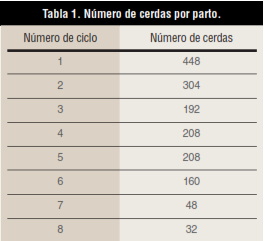
Otro uso de la distribución Chi-cuadrado es para comprobar la bondad de ajuste (Goodness-of-Fit en inglés). Por ejemplo, el número de cerdas que tenemos en una granja dada por parto viene dado por la tabla 1:
¿Es esta distribución diferente a la que nos recomienda nuestra empresa suministradora de genética, por ejemplo la que sigue la tabla 2?
Para comprobarlo vamos a ejecutar el siguiente código en la consola de R:
Unos detalles sobre la introducción de estos datos y sobre la salida. Hemos de fijarnos en que el vector “observed”, tiene los datos brutos del contaje del número de cerdas en cada parto, pero el vector “expected”, es decir, lo esperado, son las frecuencias en tanto por 1 del número de cerdas por parto. Como vemos, si sumamos estas frecuencias unitarias, la suma debe (y es) 1. Así:
En la salida nos informa de que el valor X-squared(Chi-cuadrado en inglés) es de 62,001, con 7 gradosde libertad (tenemos 8 filas y 2 columnas, y comolos grados de libertad son (nº columnas-1)x(nº filas-1), en este caso serán 7). También vemos que la
probabilidad asociada a ese valor es muy inferior
a 0,05 con lo que nuestro valor cae claramente en la zona de la hipótesis alternativa, lo que nos indica que hemos de rechazar la hipótesis nula (nuestra distribución de cerdas por parto seguía la distribución teórica). En este caso, la granja analizada no sigue las recomendaciones de la empresa de genética.En el próximo número seguiremos viendo más ejemplos útiles de cómo usar esta función y realizaremos gráficos con las distribuciones.
Archivos para descargar:











Comentarios
Publicar un comentario